논문 리뷰) SpikePipe: Accelerated Training of Spiking Neural Networks via Inter-Layer Pipelining and Multiprocessor Scheduling

ABSTRACT

1. Spiking Neural Networks(SNNs)은 에너지 효율성으로 각광받고 있으며, 다양한 훈련 방법이 연구됨
2. 훈련 과정은 기존 ANN 보다 연산 비용이 요구되지만, 이는 멀티프로세서를 통한 하드웨어 가속으로 해결 가능
3. 본 논문은 systolic array-based processors와 multiprocessor shceduling을 활용하여 inter-layer pipelining을 SNN 훈련 시 적용하는 것에 대해 제안한 최초의 논문임
4. delayed gradients를 사용한 훈련은 예측 정확도에 약간의 영향을 줌
5. 반면, 훈련 시 가속 효과는 1.6 ~ 2배에 달하고 communication overhead는 0.5 미만이었음

---

I. Introduction

1. SNN은 생물학적 뉴런을 모방하였으며 에너지 효율성이 ANN 보다 높음, IF, LIF 등 여러 가지 뉴런 모델이 사용됨
2. 본 연구에서는 LIF 뉴런을 First-order Infinite Impulse Response(IIR) filter*로 모델링하였음
3. SNN 훈련에는 STDP와 Backpropagation이 있는데, Backpropagation은 특성상 multiprocessor에 활용해서 처리량을 높이기(또는 가속하기) 어려움
4. SNN에서 훈련 가속을 위해 Inter-Layer pipelining을 제안하고 이를 위해 Delayed Gradient가 사용됨
5. 세 가지 기여:
   1. 제안 SNN 구조 훈련을 위한 역전파 방정식 산출
   2. 가변 Delayed Gradient를 사용한 Inter-Layer pipelining 달성
   3. Fine-grained Layer-wise scheduling algorithm

 

*왜 Infinite Impulse Response(IIR) filter 으로 모델링 하였는가?

1. 왜 뉴런 모델을 디지털 필터로 모델링 했는가?

 

1.1. 왜 디지털인가?

 하드웨어에서 구현하기 위함이다. 본 연구에 사용된 LIF 뉴런 모델은 미분 방정식으로 나타내진다. 이 미분 방정식은 연속적인 미분 연산을 요구한다. 그러나 처리 장치(Processing Unit)은 이를 이산적인(discrete) 시간 단계로 신호를 처리해야 하기 때문에 그에 맞게 형식을 디지털로 변경해야 한다. 즉, 뉴런 모델을 Continuous → Discrete 하게 만들어 버린 셈

 

1.2. 왜 이것을 필터라고 표현하는가?

  사실 함수라고 불러도 무방할 것이다. 필터의 정의는 "입력 신호를 받아 출력 신호로 변환해주는 장치"이기 때문. 그러나, 신호 처리 도메인에 특화되어 있다는 점에서 필터라고 부르는 것이 바람직할 것이다. 

 

2. 왜 여러 필터 중 IIR 필터인가?

 필터의 출력이 입력 신호에 영향을 받은 후, 이론적으로 무한히 길게 지속되기 때문이다. 즉, 재귀적 구조를 가지고 있음을 의미하며, 이는 LIF 뉴런 모델도 가지고 있는 특성이다. (1.)과 함께 정리하자면, LIF 뉴런 모델 자체는 연속적인 함수의 형태이다. 그리고 이는 하드웨어에서 바로 사용될 수 없다. 따라서 이를 디지털 필터로 변경해야 하는데, 여러 가지 디지털 필터 모델 중 IIR 필터가 그 특성상 LIF 모델을 가장 잘 모델링하기 때문이다. 

---

II. MODELING NEURONS FOR SNNs

요약

1. SNNs에 사용 가능한 여러 모델 중 본 연구는 LIF 뉴런 모델을 사용함
2. 미분방정식으로 표현된 LIF 뉴런 모델을 Laplace Transform을 통해 주파수 영역으로 변환함
3. 주파수 영역에서의 연속 시간 시스템을 디지털 시스템으로 구현을 위해 Bilinear Transform을 통해 이산화
4. 최종적으로 LIF 뉴런 모델을 이산 시간 시스템으로 변환된 디지털 필터 구조로 구현함

---

1. SNN에 사용되는 LIF 뉴런*을 미분 방정식으로 모델링

 

(1)

$$ C_{m}\frac{dv_{m}(t)}{dt}=i_{in}(t)-\frac{v_m(t)-V_{rest}}{R_m} $$

 

$ v_{m}(t) $: membrane potential

$ i_{in}(t) $: net input current to the neuron

$ C_{m} $: membrane capacitance

$ R_{m} $: membrane resistance

$ V_{rest} $: resting potential

 

*LIF 뉴런의 동역학

이를 풀면 $ v_{m}(t) $는 입력이 주어지지 않는다면, 시간에 따라 지수적으로 감쇠하는 $ v_{m}=e^{\tau t} $의 형태를 갖는다.

 

출처: WIKIMEDIA COMMONS

 

본 논문에서는 LIF 뉴런의 발화와 관련된 동역학이 깊게 다루어지지 않았다.

 

LIF 뉴런 모델이 무엇인지 궁금하다면 아래 포스팅을 참고해주시기 바랍니다.

[포스팅 링크]

---

2. Laplace Transform을 통해 미분 방정식을 주파수 영역으로 변환

 

단순성을 위해 $ V_{rest} $ 는 0으로 설정

 

(2)*

$$ V_m(s)=\frac{I_{in}(s)}{s\cdot C_{m}+\frac{1}{R_m}} $$

 

$ V_m(s) $와 $ I_{in}(s) $는 각각 $ v_m(t) $와 $ i_{in}(t) $를 Laplace transform한 것이다.

 

(2)를 통해 입력 전류로부터 막전위로의 전달 함수가 first-order infinite impulse response filter라는 것이 명백해졌다.

 

이 필터를 동일한 디지털 형태로 변환한 것은 bilinear transform을 사용해서 얻을 수 있다.

 

*(2) 유도 과정

(2.1)**

$$ \mathfrak{L} \left\{\frac{dv_m(t)}{dt} \right\}=s \cdot V_m(s)-v_m(0) $$

---

(2.2)

$$ C_m \cdot (s \cdot V_m(s)-v_m(0))=I_{in}(s)- \frac{V_m(s)-V_{rest}}{R_m} $$

 

$ v_m(0) $와 $ V_{rest} $는 0이라 가정

---

 (2.3)

$$ C_m \cdot s \cdot V_m(s) = I_{in}(s)-\frac{V_m(s)} {R_m} $$ 

---

(2.4)

$$ V_m(s) \cdot (C_m \cdot s + \frac{1}{R_m}) = I_{in}(s) $$

 

식 (2.4)을 정리하면 식 (2)를 얻는다

 

**출처: https://blog.naver.com/sallygarden_ee/221287818061 중 'ㄷ. 미분과 적분'

 

왜 미분 방정식을 주파수 영역으로 변환하는가?

• 복잡한 미분 연산의 단순화
• 시스템 동작을 직관적으로 분석
• 초기 조건을 쉽게 처리 가능

---

3. Bilinear Transform을 통해 연속 시간 시스템을 이산 시간 시스템으로 변환

 

(3)*

$$ H(z)=\frac{V_m(z)}{I_{in}(z)}=\frac{1+z^{-1}}{(c+\lambda )-(c-\lambda )z^{-1}} $$

 

이때 $ c=2C_{m}/T_s $이며, $ T_{s} $는 샘플링 주기, $ \lambda=1/R_{m} $이다.

 

식 (3)은 라플라스 변환을 Z-변환하는 과정이다.

 

이러한 변환은 연속 시간에서 정의된 시스템을 이산 시간으로 변환할 때 사용된다.

 

이를 위해 일반적으로 Bilinear Transform이 사용된다.

 

*(3) 유도 과정

(3.1) 연속 시간 변수 s와 이산 시간 변수 z의 관계식

$$ s=\frac{2}{T} \cdot \frac{1-z^{-1}}{1+z^{+1}} $$

$ T $: 샘플링 주기

---

(3.2) 식 (2)의 s를 z-도메인으로 변환

$$ s \cdot C_m \rightarrow C_m \cdot \frac{2}{T} \cdot \frac{1-z^{-1}}{1+z^{+1}} $$

 

식 (2)의 $s \cdot C_m$을 식 (3.2)의 z-도메인으로 치환 후 정리하면, 식 (3)을 얻는다.

---

전달 함수 $ H(z) $를 얻으면, 이를 바탕으로 디지털 필터 블록 다이어그램을 구성할 수 있다.

 

 

---

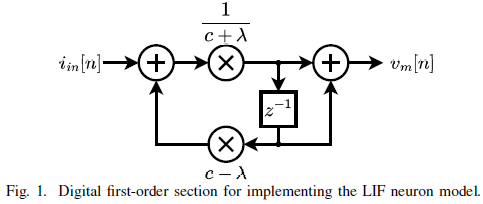
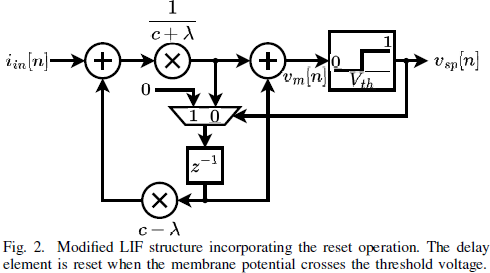
디지털로 구현된 입력 전류와 막전위, 출력 스파이크 열(Train)을 수식으로 나타내면 아래와 같다.

 

 

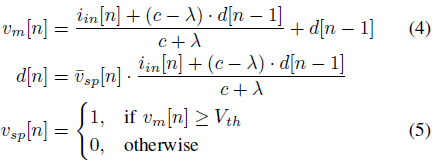
$ v_{sp}[n] $: binary time series

$ d[n] $: intermediate value stored in the delay element at timestep $ n $

$ \overline{v}_{sp} $: binary complement of $ v_{sp} $

---

III. TRAINING SNNs

1. 본 연구에서 신경망 내 요소를 표현하는 방법에 대해 정의

 

 

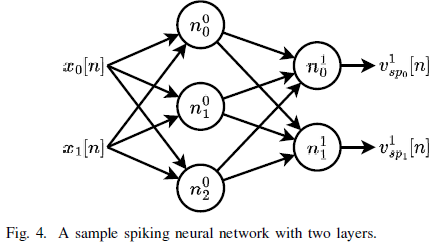
본 샘플 SNN은 2개의 레이어로 구성되어 있고, 입력과 출력 뉴런은 2개, 은닉층의 뉴런은 3개로 이루어졌다.

 

$ l $번째 레이어에 있는 $ i $ 번째 뉴런은 $ {n}_{i}^{l} $로 표현한다.

 

이 표현은 다른 중간 변수들에도 동일하게 적용된다.

 

이전 레이어의 $ i $번째 입력으로부터 $ j $번째 뉴런에 연결된 가중치는 $ {w}_{ij}^{l} $로 표현한다.

 

예를 들어, 은닉층(=0번째 레이어)의 $ j $번째 뉴런에 전달되는 입력 전류는 다음과 같다.

 

(6)

$$ {i}_{in_{j}}^{0}[n] = \sum_{i=0}^{1}{w}_{ij}^{0} \cdot x_i[n] $$

 

또한, 그림 (5)는 T 시간 단계동안 은닉층의 한 뉴런의 dataflow graph(DFG)를 펼친 것이다.

 

 

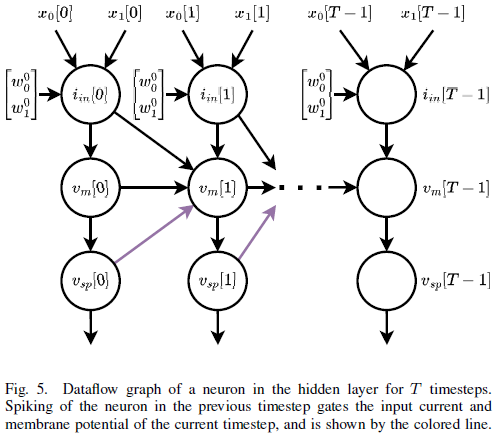
그림 (5)에서 의문점

$ i_in[0] $는 $ v_m[1] $에 단방향으로 연결되어 있다. 이것은 통상적인 RNN 레이어를 펼친 것과 다르다.

 

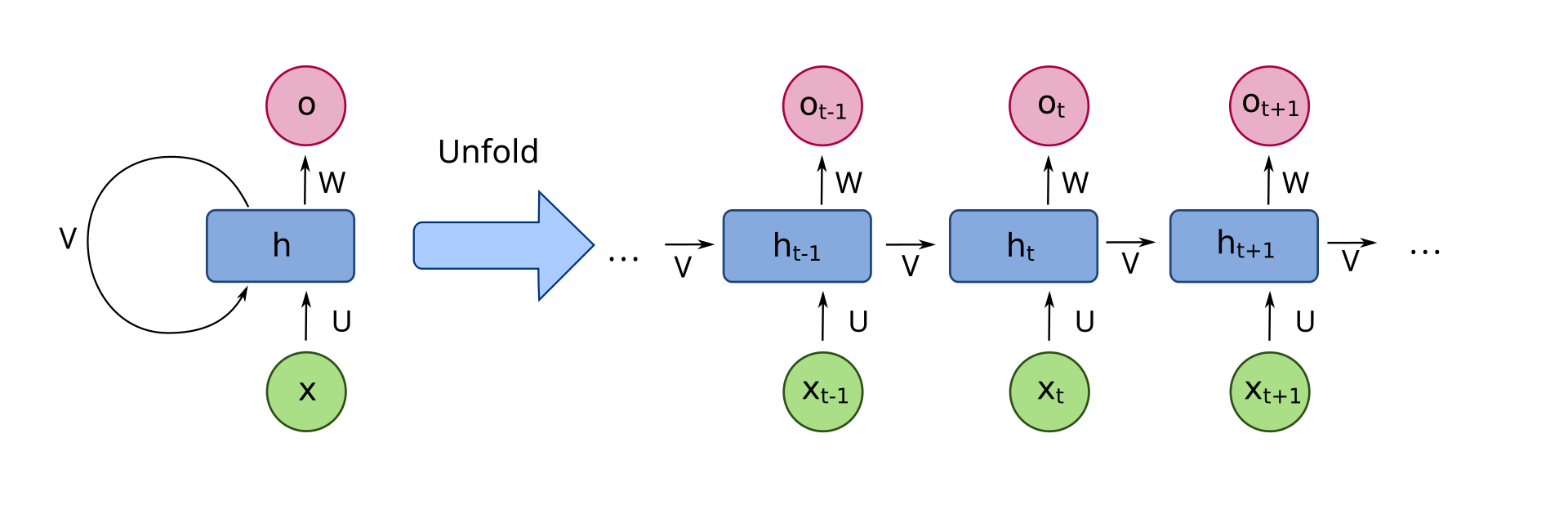
Unrolled RNN (출처: 위키피디아)

 

그림 (5)의 경우 보라색 실선으로 전달되는 값이 게이팅을 수행하여, $ i_in[0] $ 또는 $ v_m[0] $가 $ v_m[1] $에 전달된다.

 

스파이크가 발화했다면, 이전 입력 전류는 전달하지 않고 막전위가 초기화된다.

 

반대로, 발화하지 않았다면 이전 입력 전류가 전달된다.

 

단, 막전위가 초기화된다는 명시적인 구현이 그림 (5)에는 없다.

---

A. Loss Function

1. 신경망은 지도 학습을 위해 신경망의 출력과 정답 사이의 편차를 측정하는 손실 함수를 사용해 훈련됨
2. SNNs의 출력은 이진 수열(Binary Sequence)로, 정답을 이러한 형태로 인코딩하는 것은 쉽지 않음
3. 따라서, 가장 마지막 시간 단계의 출력층 뉴런의 막전위 값을 신경망의 출력으로 취급함
4. 막전위가 네트워크의 출력을 정확하게 반영할 수 있도록 출력층의 LIF 뉴런은 감쇠와 초기화 되는 기작을 제거
5. 출력 뉴런들의 막전위를 로짓(Logit)으로 취해서, 이를 Cross-Entropy Loss Function을 사용해 정답과의 오차를 측정

---

B. Backpropagation

1. 신경망 훈련을 위해 그레디언트(Gradient)를 구하는 것이 이어 요구되고, 가중치의 갱신은 경사 하강을 사용해 이루어진다.
2. 각 가중치의 손실 함수에 대한 그레디언트는 역전파를 통해 구해진다.
3. 그리고 역전파 알고리즘은 미분의 체인 룰(Chain Rule)에 기반을 두고 있다.

 

본 연구에서는 각 노드(뉴런)에 두 가지의 계산 방정식이 적용된다는 것에 주목했다.

• forward pass equation: 신경망의 출력을 계산하는 데 사용
• backward pass equation: 가중치와 중간 출력과 관련된 손실 함수의 그레디언트를 계산하는 데 사용

 

1) $ i_{in}[n] $에 대한 forward pass와 backward pass 정의

 

(9) forward pass equation

$$ {i}_{in_{j}}^l = \sum_{i} {w}_{ij}^l \cdot {v}_{sp_i}^{l-1}[n] $$

 

이는 $ n $ 시간 단계의 $ l $번째 층의 $ j $번째 뉴런으로 들어가는 입력이 같은 시간 단계의 직전 층의 발화 여부와 가중치의 곱의 합으로 이루어진다는 것을 의미한다.

 

(단순히 ANN에서 가중합을 의미하는데, 이전 레이어에서 오는 값이 1 또는 0인 것 뿐이다.)

 

(9)를 통해 중간 출력에 대한 Local Gradients를 계산할 수 있다

 

(10)

 

 

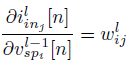
(11)

 

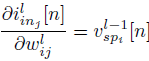
그리고 이 Local Gradients를 이용해서, Chain rule이 적용된 Global Gradients를 구할 수 있다.

 

(12)

 

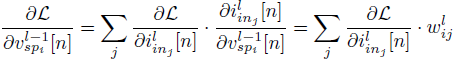
(13)

 

---

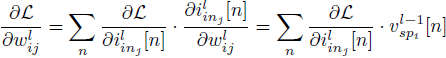
2) $ v_m[n] $에 대한 forward pass와 backward pass 정의

 

수식 (4)를 통해 forward pass는 이미 정의가 되어있으므로, backward pass만을 정의한다.

 

수식 (4)를 바탕으로 편미분을 통해 각 파라미터에 대한 그레디언트를 구할 수 있다.

 

(14)

 

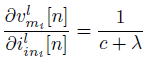
(15)

 

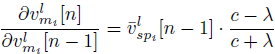
(16)

 

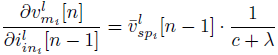
식 (17)부터 (23)까지는 생략.

---

C. Dataflow Graph of Training

 

 

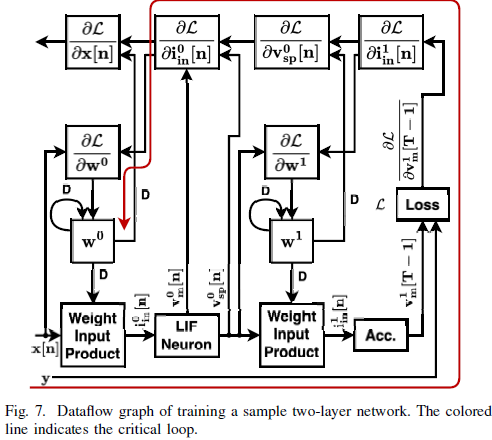
1. DFG의 각 노드는 단일 mini-batch에 대해 계산을 수행한다.
2. 즉, DFG의 한 사이클 당 mini-batch에 대한 가중치 갱신이 수행된다.
3. 해당 DFG는 ANN의 DFG와 거의 유사하나 시간 차원이 더 추가되었다.
4. Fig. 7.의 붉은색 화살표는 critical loop인데, 저 루프를 돌면 가중치가 갱신된다.
5. 이 critical loop에 지연 요소*가 한 개 밖에 없어서, 이 DFG를 그대로 multiple processor에 매핑하기 위해 retime 하는 것은 간단하지 않다.

 

*지연 요소가 한 개라는 것의 의미

지연 요소가 한 개라는 것은 경로 내 연산 요소들이 강하게 의존적이라는 것을 의미한다.

 

Fig. 7.에서 x[n]이 사이클을 돌기 시작했다면, 반드시 $ w^0 $까지는 처리되어야 하는 의존성이 있다.

---

D. Delayed Gradients

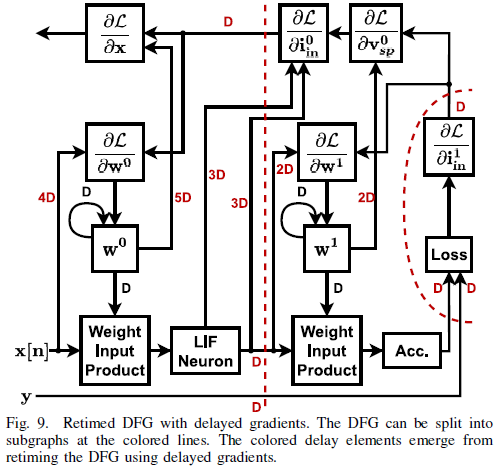
1. 해당 DFG를 서브 그래프로 나누고, 이를 multiple processors에 매핑하기 위해 지연 요소가 반드시 critical loop에 추가되어야 한다.
2. 이를 달성하는 방법은 Delayed Gradients라는 것인데, 이에 따르면 그레디언트 갱신 몇 개의 사이클 동안 지연되어 앞선 지연 요소의 추가를 달성할 수 있게 한다.
3. 이러한 방법은 선행 연구인 LayerPipe에 그 접근법이 설명되어 있다.
4. 이 방법의 적용은 네트워크의 Trainability와 Convergence에 대한 분석을 요구한다.
5. Stochastric Gradient Descent(SGD)보다 Adam에 적용하기 더 적합하다.

E. Example Networks

1. Delayed Gradients의 효과 확인을 위해, 세 가지 데이터셋에 각각 다른 하이퍼파라미터로 테스트를 수행
2. 그 결과 네트워크 규모 별로 차이가 존재 및 작을 수록 그 영향이 미미하고 클 수록 영향으로 인한 정확도 저하가 크다는 것을 확인

---

( "IV. ACCELERATING FOR TRAINING SNNs" 부터 계속 )