Pioneer
논문 리뷰) Rectified Linear Postsynaptic Potential Function for Backpropagation in Deep Spiking Neural Networks 본문
논문 리뷰) Rectified Linear Postsynaptic Potential Function for Backpropagation in Deep Spiking Neural Networks
hwkang 2024. 11. 18. 19:46게재 정보
성격: 저널
저널명: IEEE TRANSACTIONS ON NEURAL NETWORKS AND LEARNING SYSTEMS, VOL. 33, NO.5, MAY 2022
저자: Malu Zhang 외 10인
요약
- Spiking Neural Network(SNN)은 생물학적으로 타당하고, 스파이크 활용 특성 덕분에 초저전력 이벤트 기반 처리에 유용
- SNN 역시 Artificial Neural Network(ANN)처럼 심층 구조를 통한 성능 향상을 기대할 수 있으나, 실제 훈련은 ANN이 하는 것을 그대로 적용할 수 없음
- 본 연구에서는 이에 착안하여 다음과 같은 기여를 하였음:
- 왜 기존 error Backpropagation(BP)는 DeepSNNs에서 잘 동작하지 않는가에 대한 탐구
- 해당 문제를 해결하기 위한 rectified linear postsynaptic potential function(ReL-PSP) 뉴런 모델과 학습 알고리즘 spike-timing-dependent BP(STDBP) 제안
- 뉴로모픽 가속기 You Only Spike Once(YOSO)에서 제안 방법의 추론 성능에 대한 평가
I. INTRODUCTION
알려진 사실
DNN은 일부 문제 해결에 뛰어난 성능을 보이나, 고성능 컴퓨팅 자원이 요구되며 이는 전력을 중요시하는 컴퓨팅 환경에 치명적.
이에 대해, SNN은 대안이 될 수 있음
알려지지 않은 문제
SNN의 이론상 이점은 역설적으로 SNN의 특성 때문에 현실의 문제에 바로 적용되지 못함
다시 말해, 기존의 역전파 방법이 SNN에는 그대로 적용될 수 없다는 것(이에 대한 원인은 섹션 II에서 다루어짐)
과거 연구 사례
앞선 문제를 해결하기 위해 다양한 방향으로 연구가 지속, 대표적으로 3가지가 있음, 이에 대해 간단히 소개하자면:
- ANN-to-SNN conversion
- ANN을 훈련, 가중치를 갱신한 후 SNN으로 변환
- 변환 과정에 근사(Approximation)이 사용되어, 정확도가 떨어지는 한계
- Membrane potential-driven learning algorithm
- 막전위를 기반으로 역전파를 통한 훈련
- 막전위-발화 관계의 불연속 특성으로 인해 surrogate derivatives 등이 필요함
- 이 알고리즘은 Backpropagation-Through-Time(BPTT)을 기반으로 하는데, 연산 지연과 메모리 요구량이 높음
- Spike-driven learning algorithm
- 스파이크가 생성된 시점이 정보를 가진다는 견해
- 따라서, 스파이크 시점을 기반으로 그레디언트를 구해 역전파 수행
- 해당 분야의 선행 연구 사례들은 일부 문제로 인해 훈련 전략이 복잡하고 확장성에 제약이 있음
- 그럼에도 앞선 2가지 방법과 달리, 엄밀하게 이벤트 기반 처리 관점에서 동작하고 Temporal coding과 양립 가능함
아이디어 제안
요약에서 언급한 것처럼, 본 논문은 2가지 아이디어를 제시함
- ReL-PSP: 기존 훈련 알고리즘의 문제를 해결하기 위한 단순하지만 강력한 스파이킹 뉴런 모델
- STDBP: 스파이크 발생 시점에 기반해 역전파를 수행
기타
어떤 DeepSNN 훈련에 어떤 문제가 있는지, 제안 아이디어의 평가 결과는 어떤지에 대한 구체적 설명은 이후 섹션에 서술함
II. PROBLEM ANALYSIS
왜 ANN에서 사용하는 역전파 알고리즘을 그대로 사용할 수 없을까?
우선, DeepSNN이 수학적으로 어떻게 표현되는지 알아보자; 신경망 유형은 Fully-connected이다.
또한, 모든 뉴런은 순전파 과정에서 최대 한 번 발화한다.
먼저 막전위 모델의 경우:
(1)
$$ V_j^l(t)=\sum_{i}^{N}\omega_{ij}^l \varepsilon (t-t_i^{l-1})-\eta(t-t_i^{l}) $$
이에 대해 자세히 설명하는 것은 SNN 자체에 대한 포스팅에서 다루고,
간단하게 설명하자면 우항의 $\eta$ 앞 마이너스를 기준으로 왼쪽은 막전위 축적, 오른쪽은 리셋에 기여하는 항이다.
(2)

그 다음 이 방정식은 PSP function, 즉 특정 시점 t에 막전위가 어떤 값을 가질 지 결정한다.
아래 그림처럼 값이 상승했다가 다시 감쇠하는 성질이 있다.

마지막으로, 막전위가 임계점에 도달하면 발화하는 것을 정의하는 spike generation function이 있다.
(3)
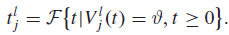
이렇게 세 개의 방정식으로 누설(Leaky), 통합(Integration), 발화(Fire) 성질을 나타낸 모델을 LIF 모델이라 한다.
이 LIF 뉴런의 발화 시점 $ t_j^l $를 통해 가중치와 이전 스파이크에 대한 그레디언트를 구하는 공식은 아래와 같다.
(4)
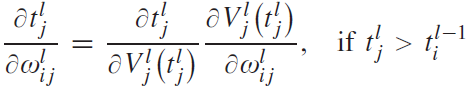
(5)
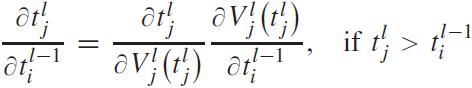
참고로 (4)와 (5)는 두 인접한 레이어 $ l-1 $과 $ l $간의 그레디언트이므로 로컬 그레디언트이다.
문제1: 미분 불가능
중요한 것은 이러한 그레디언트 계산이 (3)에 의해 미분 불가능하다는 것이다.
그 이유는, 막전위가 연속적으로 변하다가 발화 시점에 미분 불가능해지기 때문이다.
아래 그림을 참고하자.
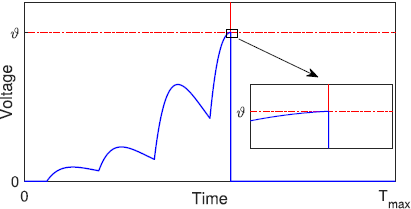
이에 대해 선행 연구는 수식 (4)를 계산하기 위해 한 가지 가정을 추가한다;
막전위 $V_j^l(t)$가 발화 직전 아주 작은 시간 간격으로 선형 증가한다.
이에 따른 수식은 다음과 같다:
(6)
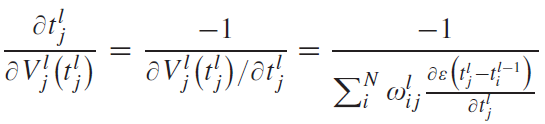
(7)
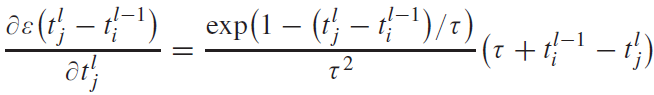
문제2: 그레디언트 폭발
다음으로 그레디언트 폭발 문제가 있는데, 이 역시 막전위와 스파이크의 관계에 의해 발생한다.
막전위가 임계점에 도달해, 스파이크를 발생시키면 그레디언트가 $ \partial V_j^l(t_j^l)/ \partial t_j^l \approx 0 $ 과 같이 되어,
수식 (6)에서 그레디언트가 무한대로 폭발해버린다.
이러한 문제를 해결하기 위해 adaptive learning rate, dynamic firing threshold가 제안됐으나 완전히 해결하지 못했다.
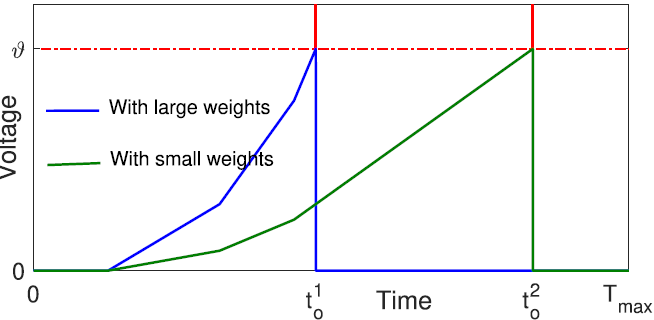
문제3: 죽은 뉴런(Dead neurons)
스파이크에 의존해 학습을 수행하는 신경망의 문제점은 스파이크가 주어진 시간 동안 발화하지 않으면 학습이 안된다는 것이다.
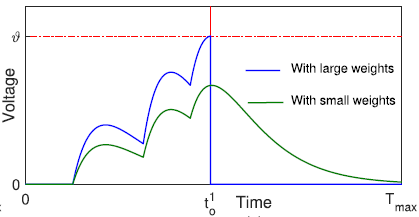
그 예시가 위 그림인데, 가중치가 충분히 크지 않은 경우 발화를 아예 하지 않고 그 단계에서 학습에 완전히 배제되어 버린다.
뉴런이 학습에 참여하지 못하는 일이 반복될 경우 궁극적으로 학습 성능이 떨어지게 된다.
이와 같이 LIF 뉴런이 포함된 SNN을 오차 역전파를 통해 직접 훈련시키기에는 문제가 있다.
이에 대해 본 논문에서 제안하는 뉴런 모델과 학습 알고리즘은 해당 문제로부터 자유롭다고 밝혔다.
III. SPIKING NEURON MODEL AND LEARNING ALGORITHM
A. ReL-PSP-Based Spiking Neuron Model
ReL-PSP란 Rectified Linear Post-Synaptic Potential의 약자이다.
간단히 말하자면 막전위 동역학(dynamics)를 부분적인 선형 함수로 모델링했다는 의미다.
이를 수학적으로 표현하면 아래와 같다:
(8)
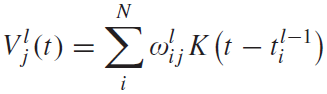
(9)
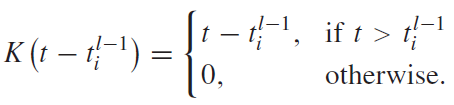
커널 함수를 표현하는 수식 (9)를 보면, 스파이크가 들어온 시점을 x 절편으로 선형적으로 증가한다.
아래 그림을 참고하자:
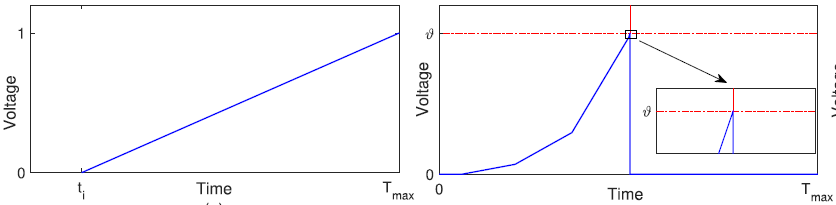
아래 그림에서 좌측은 막전위의 커널 함수, 우측은 막전위 변화 양상을 나타낸다.
해당 커널 함수를 이용해 그레디언트를 구하는 수식은 아래와 같다:
(10)
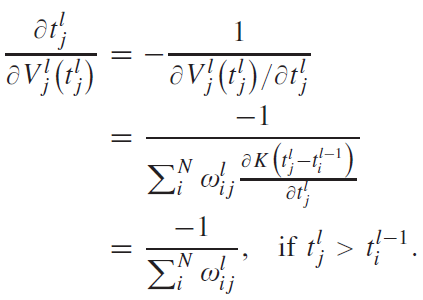
그리고 아래 수식 (11)을 통해서 완전하진 않으나 그레디언트 폭발 문제를 해결할 수 있다.
(11)
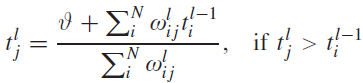
마지막으로 아래 그림과 같이, ReL-PSP는 입력 스파이크에 의해 막전위가 선형 증가하는데,
어떤 뉴런에 연결된 시냅스 가중치의 세기가 약해도 늦게나마 발화하는 것을 보장한다.
이를 통해 순전파 동안 스파이크가 하나도 발생하지 않아 발생하는 죽은 뉴런 문제를 회피할 수 있다.
B. Error Backpropagation
n 개의 범주 중 하나를 예측하기 위해, 출력층에는 n 개의 출력 뉴런을 상정한다.
이때 출력 뉴런 중 가장 빨리 발화한 뉴런이 가리키는 범주를 예측으로 취급한다.
그리고 역전파의 목표는 정답 범주에 대한 뉴런의 발화 시점을 당기고, 나머지를 늦추는 것이다.
사용된 손실 함수는 Cross-entropy이며, 출력 뉴런들의 발화 시점은 음수로 바꾼 뒤 Softmax 함수를 사용해 확률로 변환한다.
(음수로 변환된 각 출력 뉴런의 스파이크 타이밍은 가장 빠른 발화 시점이 가장 큰 값을 갖는다.)
(12)
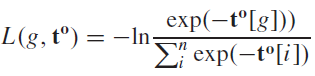
마지막으로, ReL-PSP 뉴런을 사용하는 레이어의 로컬 그레디언트 계산 수식은 아래와 같다.
아래 수식 (13)과 (14)는 DeepSNN의 그레디언트 계산에 바로 사용할 수 있다.
(13), (14)
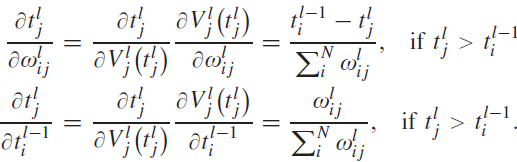
IV. HARDWARE MODEL
이 섹션에서는 You Only Spike Once (YOSO)라는 뉴로모픽 가속기에 대해 소개한다.
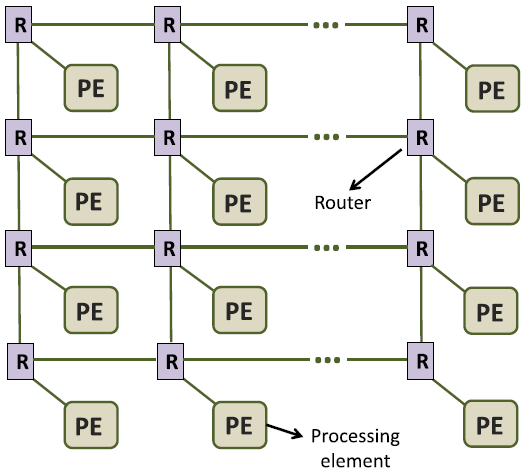
Fig. 4. (a)는 YOSO 가속기가 NoC 구조를 취하고 있다는 것을 나타낸 것이다.
각 Processing Element (PE)는 라우터와 연결되어 있어, 입력 스파이크를 받거나 생성된 출력 스파이크를 다른 노드에 전파한다.
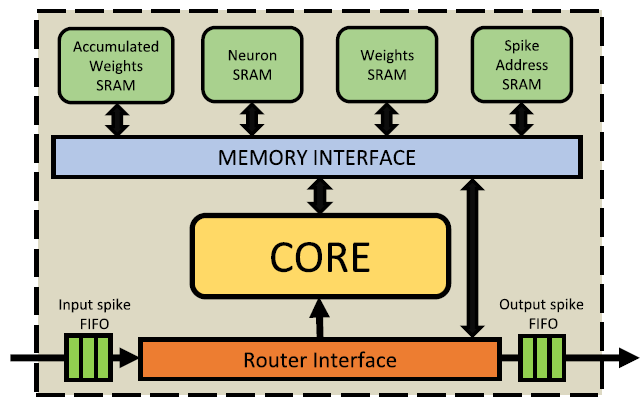
Fig. 4. (b)는 PE의 내부 구조를 나타낸 것이다.
SRAM들은 목적에 따라 나뉘어 있으며, 메모리 인터페이스를 통해 두 요소와 통신한다.
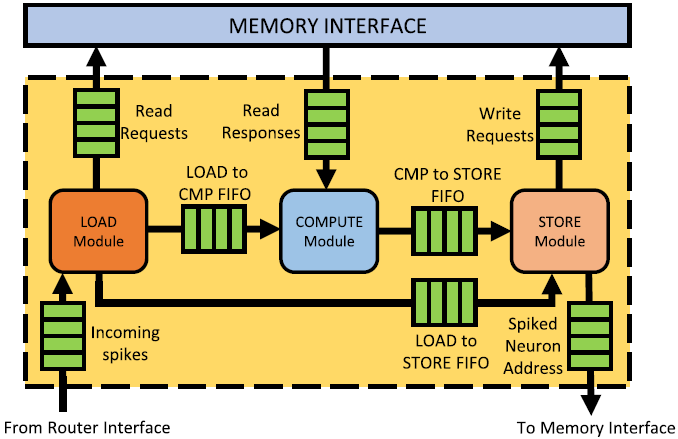
마지막 (c)는 PE 내 코어를 나타낸다.
코어에서 데이터가 다뤄지는 방식은 First In First Out (FIFO) 방식을 취한다.
중요한 것은 세 가지 모듈로 구성된다는 것이다: LOAD, COMPUTE, STORE
동작 흐름은 아래와 같다.
- LOAD 모듈에서 입력 스파이크를 받고 메모리 인터페이스에 기존 스파이크와 가중치 정보를 Read 요청한다.
- COMPUTE 모듈에 Read 응답을 받고 입력 스파이크에 대해 계산해 결과를 STORE 모듈로 보낸다.
- STORE 모듈에서 변화된 막전위에 대한 데이터를 기록하고 생성된 스파이크를 다른 뉴런으로 보낸다.
B. Mapping과 C. Hardware Simulation Methodology는 생략
V. EXPERIMENTS
실험 결과에 대해서는 요약해서 서술한다.
정확도
- MNIST 데이터셋에 대해, STDBP 방법을 사용해 네트워크를 훈련시켰을 때 Fully-Connected 모델의 정확도가 높은 편
- C-SNN의 경우 가장 높았고, single-spike-timing-based supervised 알고리즘 기준 가장 우수하다.
- Fashion-MNIST, Caltech도 동일
학습
- ReL-PSP의 경우 은닉층의 대다수 스파이크가 출력층 보다 앞서, 둘 사이 상관관계가 뚜렷했다.
- alpha-PSP와 비교했을 때 그레디언트의 분포는 ANN과 유사하게 균일했다.
- 죽은 뉴런의 비율이 에폭 수에 따라 증가하지만 그 비율은 alpha-PSP 보다 적었다.
에너지 효율성
- 다른 가속기들과 비교했을 때, 경쟁력 있는 정확도를 동반하면서 프레임 당 에너지 소비량이 우수했다.
VI. DISCUSSION AND CONCLUSION
- 본 연구에서는 DeepSNN의 BP에 대한 문제를 고찰하고 이에 대한 해결책 두 가지를 제시했다.
- ReL-PSP
- STDBP
- 해당 방법을 MNIST 등에 대해 평가한 결과 대부분 우수한 정확도를 보였다.
- Temporal coding과 양립 가능해 에너지 효율성도 매우 높았다.
- 또한, alpha-PSP 보다 구조적으로 간단해 구현이 용이하다.
- 즉, 구현을 위해 추가적인 학습 기법이 필요치 않다.
- 한편, 본 연구에서 가속은 '추론'에 대해서만 이루어졌는데, 만약 대상 워크로드가 훈련 집약적일 경우 성능 면에 한계가 있을 것으로 예상된다.
- 특히 컴퓨팅 자원이 부족한 엣지 디바이스의 경우 모델을 주기적으로 재학습 시킬 필요가 있는데, 이때 추론 가속만 가능한 것이 문제로 작용할 것
끝.


